電子顕微鏡を自作したい人のために
走査型電子顕微鏡に限れば、熱意さえあれば自作することは十分可能だと思います。
電子レンズに永久磁石型のものを使用すればレンズ電源はまったく不要です。高圧電源も加速電圧が5kV以下でしたらそれほど危険でもありませんし、1万倍程度の画像が得られます。反射電子検出器ならホトダイオードで代用できます。偏向コイル部だけは電気系の設計が必要ですが、原理的な部分だけでしたら趣味でマイコンを使ったことがあり、C言語を少しかじり、オーディオアンプを作ったことがある程度で、ビームスキャンからUSBで画像データ転送、PCでの画像表示まで、比較的容易にできます。これらについて、少しずつ紹介していこうと思っています。
その1
EXCELによる
磁界型レンズの焦点距離
収差係数(球面、色)の計算
現在、電子顕微鏡の多くは磁界型レンズを使っています。光学設計をする上で最初に知りたいのは焦点距離、収差係数です。これらが得られれば、標準的な電子顕微鏡の光学設計が十分可能です。
近軸理論を使った、レンズ定数については、裏 克己著「ナノ電子光学」(共立出版)の(4.19)式、(5.40)式、(5.43)式から、磁場分布が与えられれば、r(軸からの距離)、Cs(球面収差係数)、Cc(色収差係数)がそれぞれ求められます。(4.19)から2階微分方程式を解き、その値を使って(5.40)式、(5.43)式を使って積分するとCs,Ccが得られます。これをEXCELのワークシートで計算したものを掲げます。計算の中身が分かるように、計算の各項ごとに列を分けて分かりやすくしています。
磁場分布をZ(位置)とBz(磁束密度)の列に入力し、加速電圧Vを設定すると自動的に計算します。ZとBzは、磁場のシュミレーション結果を流し込んでもいいですし、実際のレンズの磁場を測定して入力してもかまいません。刻みをなるべく細かくして入力するといいと思います。例では、0.3mm刻みで入力しています。
rを求める微分方程式の解法では、反復計算をして収束させているところ(「オプション」の「計算方法」で設定可能)がポイントです。電子線は、この例では、軸から1mの位置で軸に平行に入射しています。1mというのは非現実的な値ですが計算結果には影響しません。焦点位置は、rの符号が+から-に変るところ(軌道が軸を切るところ)です。
焦点距離fは、焦点位置での軌道の接線と、入射ビーム直線との交点から求めています。fは、ワークシート上のセル:H6で計算していますが、焦点位置でのr’(n)のセル位置を、その都度指定してください。収差係数の計算では、焦点位置でのビーム収束角r’で割算する部分がありますが、この値は焦点位置が決るまで分かりません。それで便宜上、積分途中の各行での収束角で割っています。ですからCs,Ccの値に意味があるのは、焦点位置での値だけです。この割算の部分があるので入射条件のビーム位置によらず、最終的な計算結果はいつも同じ値になります。このことは、焦点位置での収束角が45°(r’=1)となるような平行ビームが入射した時の収差を収差係数とする、と言い換えることもできます。
この計算法で、他のレンズ計算ソフトとほぼ同じ値が得られています。しかしながらまだ数例しか応用例がありません。バグ情報やご意見などありましたら、是非お寄せください。なお、このソフトはご自由にお使いいただけますが、性能を保証するものでもありませんので、参考程度にお使いください。
この計算法を使って、皆さんもご自分で電子レンズを作られては如何でしょうか。
一度とにかくレンズを作って磁場測定をすればレンズ定数が計算できます。それを元にレンズ形状を変えて、どのように定数が変化するかを経験すれば、レンズというものが肌で分かるようになると思います。
その2
永久磁石型電子レンズの設計法
電磁型電子レンズに関する文献は多いのですが、永久磁石型のものについては少ないです。私が見つけた文献を三つほど紹介します。
1. 木村:日立評論 Vol.39 No.3(1957)
電子顕微鏡の永久磁石励磁方式とその特性
かなり古い文献ですが、永久磁石レンズの概要がわかります。
2. Klemperer:ELECTRON OPTICS(1953)
5-4 Practical lens design の最後の方、数ページに永久磁石レンズの説明があります。
3. P.W.Hawkes:Toppics Current Physics (Magnetic Electron Lenses)(1982)
4.6章 Permanent-Magnet Lenses に20ページ程度の解説があります。磁場の強さを機械的に変更する構造についていくつかの例が示されており、実際に設計する際に参考になると思います。
これらの文献を引用し私がある学会で発表したTinySEM紹介の原稿がありますので、ご覧ください。文献を入手できなくても、これでおおよその構造が分かると思います。
TinySEMの紹介(PPT)
その3
偏向コイルの設計(1)
結論を先に言ってしまうと、加速電圧15kV程度の小型SEMでは、内径20mm、高さ10mm程度の手に入りやすいトロイダルコアを4分割してφ0.3~φ0.4のエナメル線を1層キッチリ巻くと電流1A程度でほどよく振れるX,Y偏向コイルになります。
それでは、まず一様磁場の中に磁場方向に直角に電子が飛び込むと、電子が円運動するところから始めます。磁場の作用で、運動する荷電粒子には次式で与えられる力が作用します。
F = qv×B
(qは、電子の場合 ?e になります。)
電流方向から磁場方向に右ネジを回した進み方向に力がかかります。電流方向は電子の場合、運動方向の逆ですので注意が必要です。
フレミングの左手の法則を使うと、電流方向を中指、磁場方向を人差し指方向に合わせると、親指方向に力が作用する、という表現になります。
力のバランスの式から、次式が得られます。
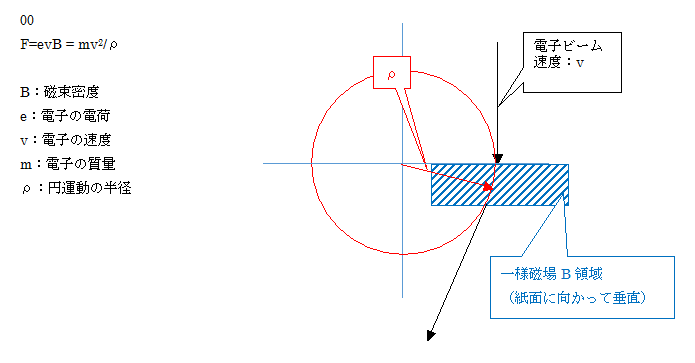
この式を変形すると、
Bρ = (m/e) v
となり、m/e(電子の比電荷の逆数)は定数なので加速電圧が決まればvが決まりますから、Bρの値は一定になります。これを、昔のSEM屋さんは、「○○kVでは、エイチローは、何ガウス・センチだったっけ」のように言っていました。どういう訳かビーローと言わないでエイチローと言っていました。HとBの違いを上手く説明できませんが、真空中では B=μ0H の関係があります。Bは磁束密度、Hは磁場の強さと説明されますが、昔の単位系ではμ0が1でしたので、BとHを混同する時があります。
私の昔(30年以上前)のメモは以下の表現になっています。
Hρ = K
K = √(11.376V) V:加速電圧
ちなみに15kVでは、Hρは413ガウス・センチになります。イメージで言いますと、50ガウスの磁場で半径8cmの円を描いて廻ります。
今では、4.15×10(-4) T・mというのが正しいですね。
この値を使うと、5mTの一様磁場Bの中を10mm電子が走った場合、おおよそ10/80=1/8 ラジアン(1rad=60°として約8°)曲がりことがわかります。偏向コイルを抜けると電子は直進しますから、偏向コイルから試料までの距離が24mmだとすると片側で3mm振れるということになります。実際のSEMとそれほどかけ離れていない値です。(続く)
その4
偏向コイルの設計(2)
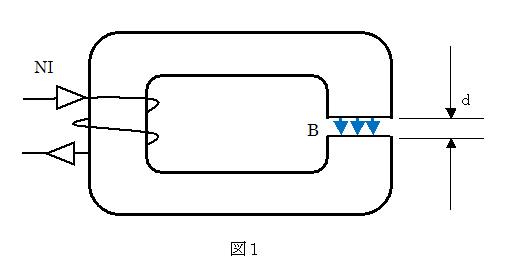
図1に示すようなコイルの場合、ギャップ部の磁束密度Bは、
B =(μ0)NI/d :μ0(真空の透磁率) = 4π・10(-7)
:NI コイルのアンペアターン
:d ギャップ部の長さ
で与えられます。(磁路のμがμ0に対して非常に大きいと仮定)
これから、
NI = (B・d)/(μ0)
となりますので、
B = 5・10(-3) T
d = 20・10(-3)m
を代入すると
NI = 80(アンペア・ターン)
となります。これは1Aの電流を流すとしてコイルを80回巻けばいいということになります。
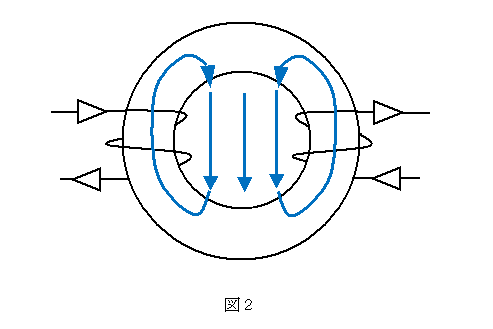
図2のような具体的なトロイダルコイルで考える場合、ギャップの長さがどこでも20mmではなく20mmより短く見積もらねばならないと気付きます。従って80アンペアターンより少ない値で5mTを実現できるのですが、上記のNIの値に 1/α を掛けることで補正します。
このαの値は、1.3くらいです。この場合は 80 × 1/1.3 = 62 となります。
すなわち、トロイダルコアの左右にそれぞれ31回ずつ巻けばギャップ部に5mTの磁場が得られます。これは、実際に巻いてみるとわかりますが、φ0.3~φ0.4のエナメル線で内径20mmのトロイダルコアちょうど1層巻くくらいの回数です。
以上より、最終的なX,Y偏向コイルの外観は3図のようになります。図の左右2対のコイルがX方向、上下2対のコイルがY方向のビーム偏向に関係します。

その5
IN/√E(アイ・エヌ・ルート・イー)の話
レンズ設計に於いてもこの値がとても重要です。
文献によってはk2やK2という係数を用いているものもありますが本質は同じで相互に変換もできます。レンズ特性の係数となるので、“レンズ強度”と呼ばれています。
この値から計算されたレンズ特性値(焦点距離、収差係数など)がテーブルの形で文献にのっています。
(例:ELECTRON BEAMS, LENSES, AND OPTICS(El-Kareh and El-Kareh))
レンズ形状に関するパラメータもありますので、最終的にはレンズ強度とレンズ形状からレンズ特性が分かるということになりますが、難しいレンズ理論を知らなくてもテーブルを見るだけでレンズ設計ができとても便利です。
慣れてくるとIN/√Eの値を聞くだけでどんなレンズを使っているのか大体わかるようになります。
その6
電子銃(その1:熱電子放射)
この方面にはいろいろな教科書(例:金持徹 編 固体電子論(裳華房))が出ていますが以下の疑問を解いてくれます。
(1) どうして金属の中の電子は勝手に出てこないのか。金属内電子はどういう状態におかれているのか。
(2) 温度を上げるとどうして電子が出てくるのか。
(3) もっとたくさん電子を出すにはどうしたらいいのか。
これらの教科書を読み進むと熱電子放出の基本式が出てきます。それが有名な、Richardson-Dushmanの式です。例に示した参考文献では、フェルミ球の概念を使って丁寧にこの式を誘導しています。
この式から、電子源の材料と温度か決まると単位表面積から放出される電流が求められます。
Richardson-Dushmanの式
j = a・T(2)・exp(-eφ/(kT))
a :Richardson定数
eφ:仕事関数 (eV)
k:ボルツマン定数(8.6・10(-5) eV/K)
T :温度(K)
タングステンの場合、
a = 120 A.cm(-2).deg(-2)
eφ= 4.54eV
ですので、2600Kを代入すると、おおよそ1A.cm(-2)であることが分かります。
たくさん電子を取り出すには、Richardson定数が大きく仕事関数が低い材料を選び、温度を上げればいいのですが、あまり温度を上げると寿命が短くなりますので注意が必要です。
LaB6(六ほう化ランタン)は、仕事関数がタングステンより低いので良い電子源ですが、高い真空度が必要なことや、高温で活性なので非金属で挟む必要があるなどタングステンほど簡単には使えません。海外の小型SEMでは、LaB6より優れた点の多いCeB6(六ほう化セリウム)を使用しているものもあります。
その7
電子銃(その2:輝度の不変性)
この話とは別に、電子線の輝度(β)が以下のように定義されています。
β= ⊿(2) i /(⊿s・⊿ω):()は指数を示す
ここで、光軸の周りの微小面積⊿sを通って微小立体角⊿ωを通る電子流を⊿(2) iとしています。
この輝度は、ビームのどの位置でも不変という理論があります。この輝度とカソードの放射電流密度jとの関係は、以下の式で与えられます。
β= (j/π)・(eφ/kT) A/(cm(2)・str)
ここで:
eφ :加速電圧
k =8.6×10(-5) eV/K (ボルツマン定数)
数値を代入すると分かりますが、タングステンの場合、eφ = 20keV、T = 2800Kでおおよそ1×10(5) A/(cm(2)・str)となります。この条件下で、試料上のスポット径(すなわち⊿s)、対物絞り径とWD(ワーキングディスタンス)(すなわち⊿ω)を与えると、試料に流れる電流i は決まってしまいます。
1例を示しますと、
β= 1×10(5) A/(cm(2)・str) として、
対物レンズの絞り100μm、WD=15mm、試料上のスポット径20nm とすると、試料電流は、
⊿s = 1/4・π・d(2) : d = 2・10(-6) cm
⊿ω =π・α(2) : α = 50/15・10(-3) rad
から、
i = β・⊿s・⊿ω = β・1/4・π・d(2)・π・α(2)
= 10pA
と計算できます。
途中にどんな光学系を組もうが、最後の対物レンズ周りの数値だけで試料電流が計算できるところが面白いと思います。逆に試料電流をこれだけ欲しいという場合、スポット径や開き角をどれくらいにすれば良いかも計算できます。
参考文献: 上田良二 編「電子顕微鏡」,協立出版、1986.
その8
電子回路(その1:走査信号(1))
SEMの回路設計では、ハンダ付け技術やオームの法則から始まり、インピーダンスと周波数、トランジスタ回路(hパラメータと3種の接地回路)、オペアンプ回路、ボード線図によるゲイン/位相解析、回路アースとノイズの関係、など多岐にわたる基礎的な知識が前提となります。私は1970年代から1990年代頃はトランジスタ技術という専門誌で勉強しました。そのうちのいくつかの記事は単行本となって発行されています。トランジスタ回路は、コレクタ接地(エミタフォロワー)やエミッタ接地から入ってベース接地が設計できるようになると、回路設計の本当の面白さが分かりだすと思います。
トランジスタ回路の基本を理解した人でしたら、落合萌著「オーディオ用半導体アンプ設計・解析」(誠文堂新光社)は、ベース接地回路の話も多く実践的で面白い本です。オペアンプが使えても、やはりトランジスタ(FETも含めて)は電子回路の基本かと思います。
さて、走査信号の話から始めます。ビームを2次元のX,Yに振るための信号です。
走査信号は、X,Yのこぎり波発生器(鋸歯状波、スイープ波形、ランプ波形などと表現される場合もあります)を作って偏向コイルにその波形に応じた電流(磁場)を流します。オーディオアンプのように電圧ではなくて電流を制御するところに注意する必要があります。コイルに流れた電流を抵抗で受けてその電圧をフィードバックします。コイル負荷ですから位相が回って発振しやすいので苦労することが多いです。
走査信号の振幅を小さくして、それに応じてコイルに電流を流せばSEM倍率は上がります。
小型SEMでは、倍率を10倍くらいから数万倍くらいまで変えますので3桁以上振幅を変えることになります。基準信号が±10Vの走査信号であるとして、もっとも倍率を上げると1mVオーダーの振幅になり回路ノイズの影響を受けやすくなります。それで電流検出用の抵抗の値を何段か切り替えて使用します。面倒なのは、この切り替えにより負荷インピーダンスが変わり位相が変化し発振する場合があることです。
帯域を伸ばしながら位相余裕を持たせるのが難しいところです。
また、コイルで発生した磁場が有効に電子ビームに伝わらず、回りの金属部品に渦電流損として消費されることも注意が必要で、像の歪(特に左端)となって現れます。
その9
電子回路(その2:走査信号(2))

-
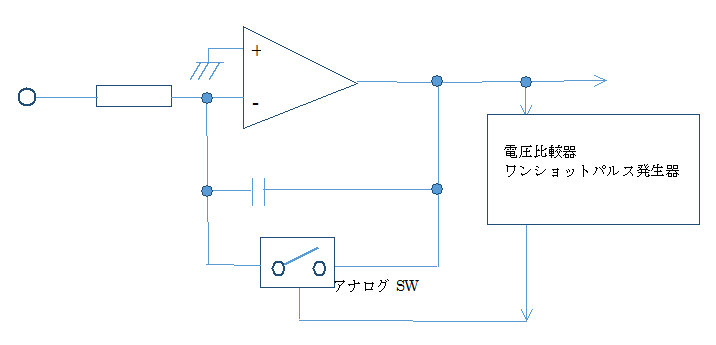
アナログ方式
スイープ波形はアナログの積分回路で簡単に作ることができます。部品点数も少なく手っ取り早く走査信号を作る場合に便利です。簡単な回路を下図に示します。
-
デジタル方式
昨今ではデジタル方式が主流と思います。Y方向のスイープは数分以上になることもありアナログ方式では洩れ電流が原因で波形が歪みやすいのですが、デジタル方式にするとその問題は解消されます。簡単にはデジタルカウンタとDACとの組み合わせで実現できます。X方向は画素クロックでY方向はX同期信号でカウントアップします。横方向で512画素以上は欲しいのでビット数は少なくとも10ビットは必要です。マイクロプロセッサーを使う場合、Y方向走査用のカウンタがソフトウェア処理で間に合えばYカウンタ回路は不要になります。波形データを予めメモリに書いておいて、そのデータをDMAでDACに順次転送する方法もあります。波形発生器でよく使われるこの方法は任意のスイープ波形が作れますので、X,Yを組み合わせて円を描くこともできます。 -
倍率制御
スイープ波形ができたとして、SEMの倍率を変える場合は振幅を変えなければなりません。乗算型DACを使って振幅をデジタルで制御することで実現できます。簡易的には抵抗切替やVRで振幅調整してもできます。 -
電流ブースター回路
どの方法でも、最終段の偏向コイルに電流を流す部分は電力回路が必要です。
パワーMOSFETを使うと下図のような電流ブースター回路になります。バイポーラトランジスタをダーリントン接続で動作させる方法もあります。
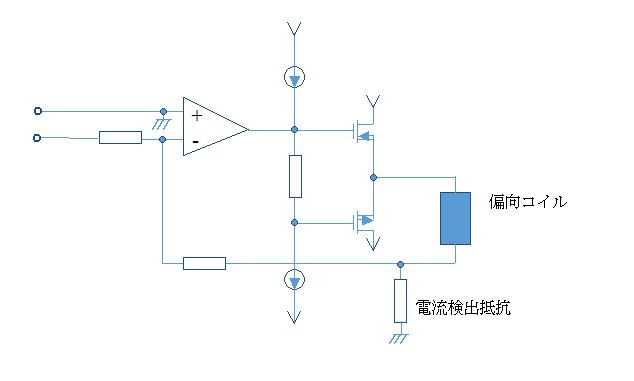
その10
電子回路(その3:画像表示)
-
アナログ式
昔のSEMは、ブラウン管の走査とSEM鏡筒の走査を同期させ、ブラウン管の輝度に像信号を入れて表示していました。スロースキャンではブラウン管の蛍光体の残光特性を利用して暗室で観察しました。同じような方法を、実験室レベルで測定器などを組み合わせて実現する例を説明します。
まず、X,Yの走査信号用のファンクションジェネレータと旧型のアナログ式オシロスコープ(Z(輝度)端子)が背面に付いているもの)を用意します。ファンクションジェネレータを使って、X,Yのスイープ波形を発生させ電流ブースタ回路で偏向コイルに電流を流します。オシロスコープのX,Yにスイープ波形を入力し、XYモードに設定します。またSEMからの像信号をZ端子に入力します。振幅や像の輝度を調整するとオシロスコープの画面にSEM像が見えます。スキャンが遅いと残像が短いので肉眼ではよく見えません。カメラのバルブ機能を使って長時間露出をして撮影します。倍率の変更は、偏向コイルに流す電流を可変します。
実際には、像信号は必要に応じて反転させる必要があるかもしれません。また、ビームが振れ戻る時にオシロスコープの像信号をブランキングする必要もあります。綺麗に像を表示するにはそれなりの改良が必要ですが、とにかく像を見たい場合に手軽に使える方法です。
レトロな方法ですが、一度経験しておくといいと思います。 -
デジタル式
汎用的なパソコン用の計測ボードが各社から出ています。これらを使ってパソコンからX,Yのスイープ波形を出力し、AD変換ボードを使って像を取り込めば、パソコンソフトで画像が表示できます。画像取り込みが低速でいいのなら、この方法が簡単でほとんど買い物で済みます。
SEMファームウェア用に別途マイクロコンピュータシステムを開発する方法もあります。いわゆる組み込みシステムですが、自作派ならばこの道を選びたいところです。最近は開発環境が無償で提供されているものもあり費用がかからなくなりました。また、ADCやDAC、DMAなどの周辺もワンチップに入ったものも多く出回っており、簡単な周辺回路を付けるだけで高度な機能を実現できます。作り込むと汎用ボードでは実現できない高速データ収集&転送が可能になります。
画像表示としては、組み込みシステム側でSEM像を表示する方法と、パソコンにデータを送ってパソコン側で表示する方法が考えられます。後者の場合は高速で画像をPCに転送する必要があります。
各社からこの手のMPUやボードが出ており、どれを使うかは迷うところです。しかも日進月歩でどんどん新しいものが出ていますので、いつも動向には目を向ける必要があります。 -
SEM像のノイズ対策
SEMの像信号はノイズが多いのでノイズを減らす工夫が必要です。ブラウン管時代は塗布された蛍光体が積算していたのですが、デジタル方式では積算やフィルタ演算が必要になります。
高速スキャンでは、リカーシブフィルタと呼ばれる蛍光体の残光特性を模擬したようなフィルタが使われます。比較的簡単な式でFPGAでもソフトウェアでも実現可能です。低速スキャンでは、主にピクセル加算が行われます。
その11
非点収差補正
はじめに非点収差の物理的意味を説明します。
電子ビームの近軸軌道計算では、2次以上の微少量を無視しますが、3次まで含めた計算をすると(2次項は理論上消える)ザイデルの幾何収差と呼ばれる(3次)収差が現れます。この中の
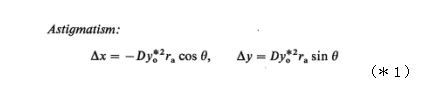
で表される量が非点収差です。これを図解したものが下図です。
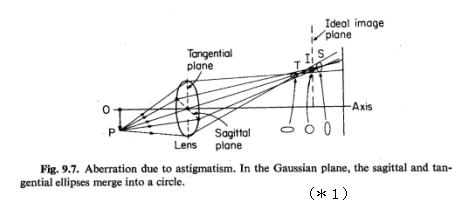
非点収差の式で、オブジェクト面の変位はyo*(上図のOP)としています。raとθは絞りの極座標です。⊿xと⊿yで符合が違うことは、X 軸方向のフォーカスとY方向のフォーカスが近軸像面から前後にずれていることを意味します。このずれは非点隔差と呼ばれます。なお、上図のIで示された位置でイメージサークルが最小なり、それを最小錯乱円(disk of minimum confusion)と呼びます。
実際に像がどう見えるかは、スポーク付車輪の分かりやすい例があります。(下図)
左図はタンジェンタル焦点面で、リムは太らないで見えますが、スポークがぼけて太く見えます。右図のサジッタル焦点面ではその逆になります。
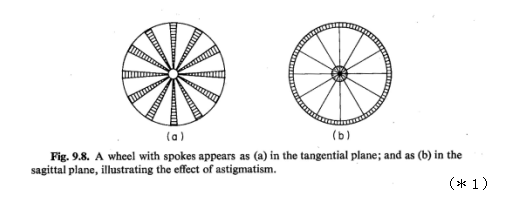
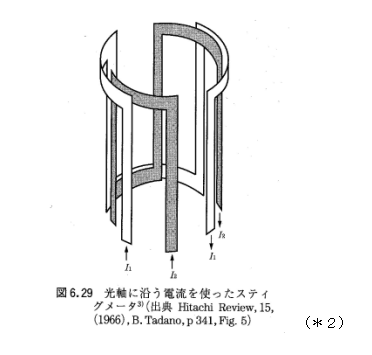
実際の非点収差は数1000倍以上でないと分かりづらく、レンズの機械的誤差もあり、この像のほんの一部(しかも中心でない部分)を拡大して見ることになります。したがって、このスポーク付車輪の例のように回転対称のボケではなく、あたかもX,Y2方向に像が流れるような現象で観察されます。フォーカスを前後に動かすと、直行する2方向のどちらかにフォーカスがあうような動きをします。非点隔差分離れた90°配置のシリンドリカルレンズ(かまぼこ型レンズ)セット(2個)ができたと表現することもできます。
この非点収差は、下図のように4極子を45°配置で2組配置することによって任意の方向の非点が補正できます。感覚的には、X方向のフォーカスを伸ばし、Y方向のフォーカスを縮める作用がビームに働くことを、フレミングの法則(ローレンツ力)で理解できますので、やってみてください。(偏向コイルの設計(1)参照)
レンズ的な見方をすると、非点収差で発生したシリンドリカルレンズセットを4極子レンズで作られるシリンドリカルレンズセットで相殺するとも表現できます。
出典:
(*1)A.B.El-kareh & J.C.El-kareh : Electron Beams,Lenses, and Optics, Vol 2 (Academic Press)(1970)
(*2)裏 ほか:電子・イオンビームハンドブック(第3版)
日本学術振興会第132委員会編(1998)日刊工業新聞社
その12
電子回路(その4:フィラメント電源)
昔のブラウン管はアノードが正の高電位、電子銃部はほぼグランド電位で、SEMとは逆になりますので注意ください。
カソードにはフィラメントを加熱するための低電圧の電源(数V、数A)が必要になりますが、SEMでは高電圧下で動作するようにフローティング電源にする必要があります。
高電圧の発生には、コッククロフト・ウォルトンの回路を使います。絶縁やノイズ、安定度の対策が必要でそれなりの経験が必要です。自作される場合は感電の危険も伴いますので十分注意してください。
高電圧電源ユニットは市販品を購入し、これにフローティングのフィラメント電源だけを自作して付ける方法が簡単です。
ここでは、高周波トランスの設計法を述べてフローティング電源を作る方法を説明します。
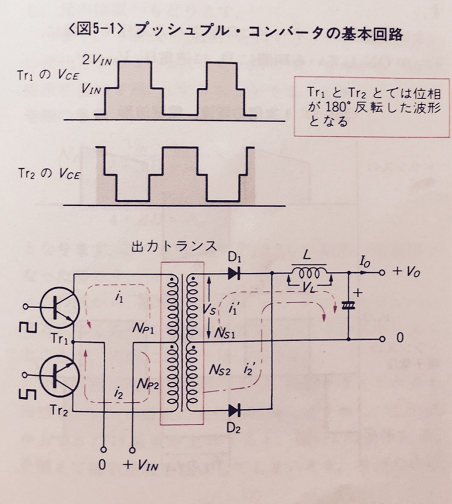
下図(*1)にプッシュプル・コンバータの回路図を示しますが、フィラメント回路もこれで設計できます。
図ではバイポーラTrを使用していますが、今はFETを使うことが多いと思います。発振回路は、どんなものでも構いません。
一次側の巻数Npは以下の式で与えられます。(*1)
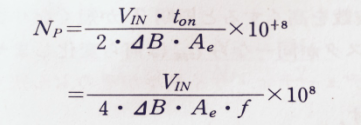
出力トランスとして、断面積(Ae)が50cm^2 程度のリング型のフェライトコアを用意します。
例として、Vin = 24V, ⊿B = 2500Gauss, Ae = 5cm^2, f = 35kHz を代入すると Np = 14 となります。
プッシュプル型の巻線は、2本(A,B)同時に巻き、Aの巻き始め1本とBの巻き終わり1本を接続するような配線をすると簡単です。
二次側は、普通のタングステン線フィラメントφ0.1mmでNs = 2~4 くらいで動作すると思います。二次側のチョークコイルは20μH 程度になります。
下図に実例を示します。二次側の線材はシリコンの耐圧電線を使っています。

スイッチング電源の参考書はいくつも出版されていますので式の導出などは追いかけてみてください。本によって単位が違う場合があり、間違えると桁違いになりますので注意が必要です。例えばAeとしてmm^2かcm^2か、B(磁束)としてgaussかmTか、などです。また、トランスの設計ではいつも磁束を飽和させないように注意します。
ここで紹介した回路は巻数が少なく作りやすいので、スイッチング電源入門のいい勉強になりますし、SEMの高圧電源を作るうえでとても実用的です。ただ、二次側は高圧になりますのでモールドしたりして絶縁には気を付けてください。実際に別に用意した負の高圧電源に接続する場合、フィラメント出力回路のセンター電位を接続します。その時、ウェネルトのバイアス電位を得るために数MΩの抵抗を直列に繋ぎ、高圧電源側をウェネルトに接続します。4MΩのバイアス抵抗を使うと、エミッションが150μAの時、600Vのバイアスがかかります。
最後に感電について経験をお伝えしておきます。感電などしないほうがいいし、したくもないのですが、私のように電気の知識も生半可な少年時代からやってきた者で感電したことがない人はまずいないと思います。私もコンデンサに充電されていた高電圧に触れ、とても大きな衝撃を体験したことがあります。小型SEMは15kVもありますが、電流が少ないのでそこまでいかないようです。しかしながら、そこそこしびれます。SEMを作っていて死亡した人を聞いたことはありませんが、十分注意してください。トランスメーカーの知人は、感電事故で死亡しました。
感電は教訓です。実験する時、高圧に限らず最新の注意を払うことは言うまでも無いのですが、心構えとして実験中は精神的に落ち着いていること、落ち着いていない時は実験しないこと、も大切な事だと思います。
出典
(*1):戸川治朗:実用電源回路設計ハンドブック、トランジスタ技術増刊、CQ出版 1988
その13
SEM画像に着色する(1)
今回からしばらく装置設計の話を離れ、SEM画像に着色する手法について触れたいと思います。弊社サイトのトップページに、西永奨さん(故人)が撮影、彩色したSM写真が表示されます。ときおり、この着色はどのように行っているのですか、という質問を受けます。実際に西永さんが色付けしている作業を見たわけでもなく、またその当時はそれほど興味も無かった(自分でやろうと思わなかった)ので、Photoshopで色付けしている、くらいの認識しかありませんでした。
日本でSEM写真を芸術の域まで高めた第一人者とされる彼が亡くなり、多少でも彼のことを知る人間として、自己流とは思いますが着色の手法をお伝えし、少しでも多くの人にSEM画像を親しんでいただけたらと思います。
さて、最初にSEM画像の画像データに付いて説明します。
ビームを走査して得られる検出器からのアナログ量をデジタルに変換し、画像メモリに順次書き込みます。簡単には8ビットのADコンバータを使いますので、値としては0から255の値のどれかになります。このままでは、単に数値がメモリ内に溜まっているだけなので、何らかの方法でモニタ上に表示して「絵」として表示することになります。モニタは、通常R(赤),G(緑),B(青)の3原色のドットで1画素が表示されます。また各色、8ビット(26階調)で表示されますので、都合2の24乗=1,600万色の発色が可能です。SEM画像の0から255のデータをどの色で表示するかは、コンピュータのプログラムに依ります。普通は、グレースケール表示なので、
SEM(0)=R(0):G(0):B(0) ;真っ黒
SEM(1)=R(1):G(1):B(1)
SEM(2)=R(2):G(2):B(2)
・・・・・
SEM(255)=R(255):G(255):B(255) ;真っ白
のようにRGBに対応させます。
ここの部分のプログラムは、例えば次のように書きます。C言語を知らなくても、ある程度ご理解いただけると思います。
for(i=0;i<256;i++){
lpRGB0[i].rgbRed=lpRGB0[i].rgbGreen=lpRGB0[i].rgbBlue=i;
lpRGB0[i].rgbReserved = 0;
}
1600万色もある中で、グレースケール表示に関係するのはRGBが同じ値である、たったの256種類しかないことは驚きです。色のある世界がいかに人間の感情を豊かにしているかを感じます。
この対応付けは、インデックステーブルとかルックアップーブル(LUT)と呼ばれます。Photoshopでは、グラデーションマップと呼んでいます。このテーブルの設計次第で自由に色の付いたSEM画像が表示できます。
ImageJというNIHから出ている無料の画像処理ソフトがあります。このソフトでSEM画像を読み込み、標準で持っているLUTで色付けする方法は最も簡単な着色法です。NIHのサイトから追加のLUTもダウンロードできますので、ほとんど困らないくらいの色付けが可能です。これだけでも、十分SEM画像の着色が楽しめます。(続く)
その14
SEM画像に着色する(2)
前回説明したLUTを使って着色した例を紹介します。
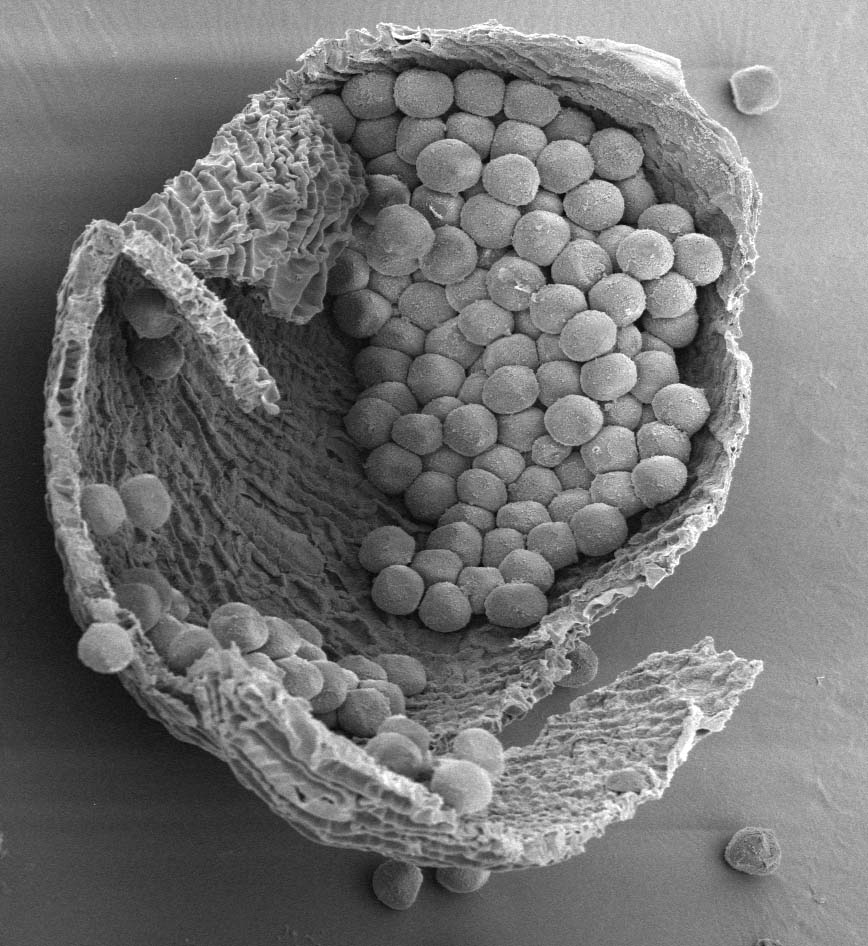 |
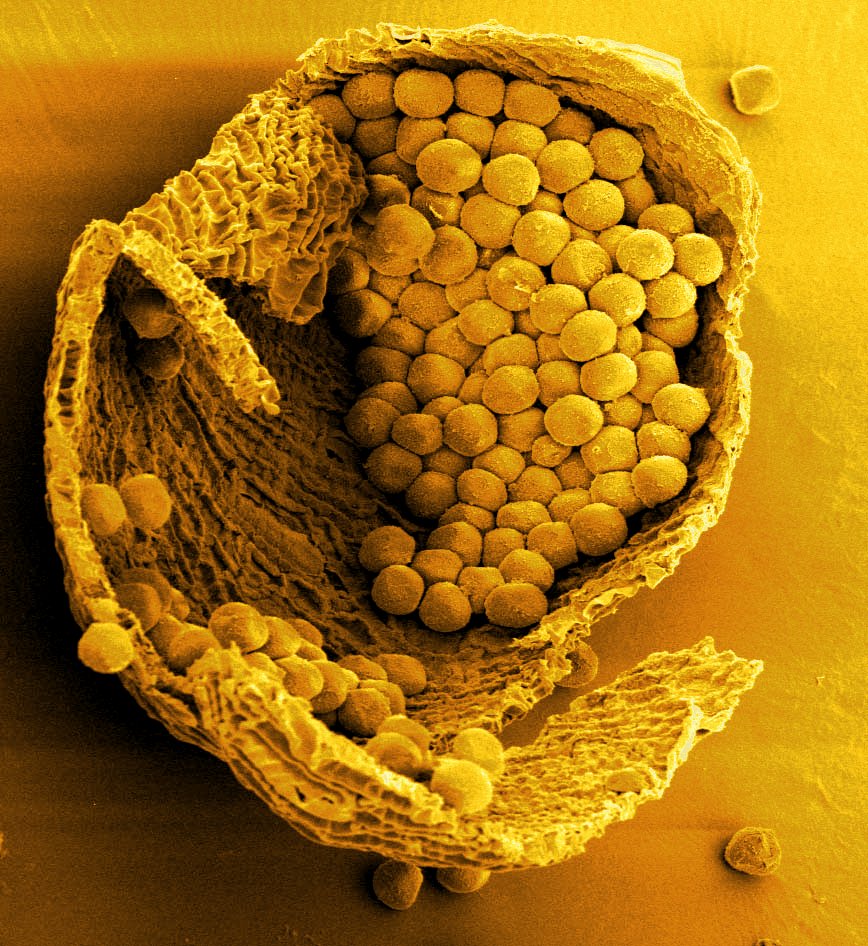
| 図1 スギ花粉 |
図1は、スギ花粉が葯に入っているSEM写真です。
これをLUT機能を使って着色してみましょう。
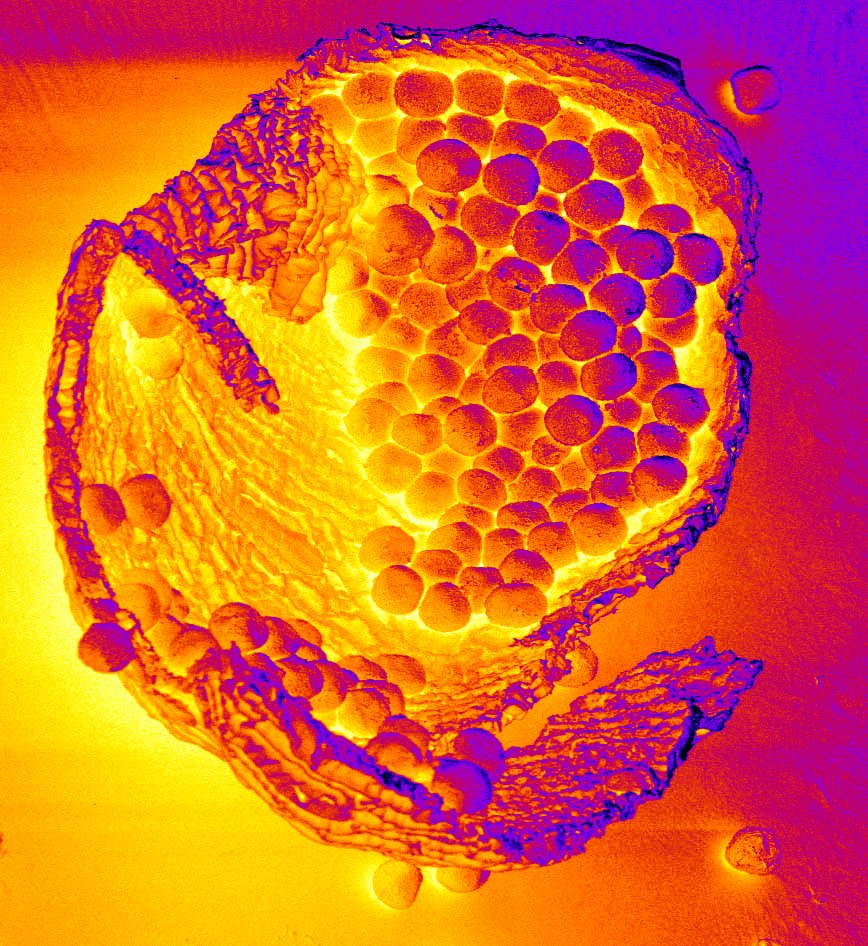
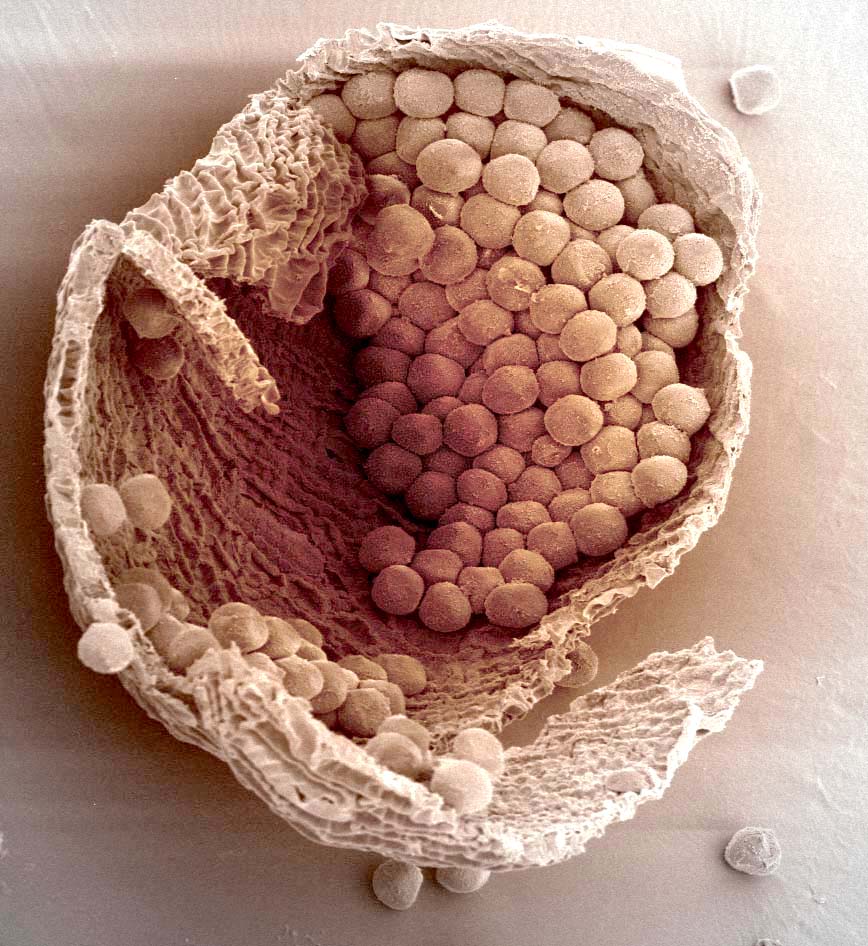
図2、図3は、ImageJで提供されているLUTをそのまま使っています。図4は私が作製したセピア調のLUTで着色した例です。この方法は画面全体にインデックステーブルが適用されますので、部分的に色を変えたい場合はさらに別の手法が必要になります。これについては、おいおいお話します。
 |
 |
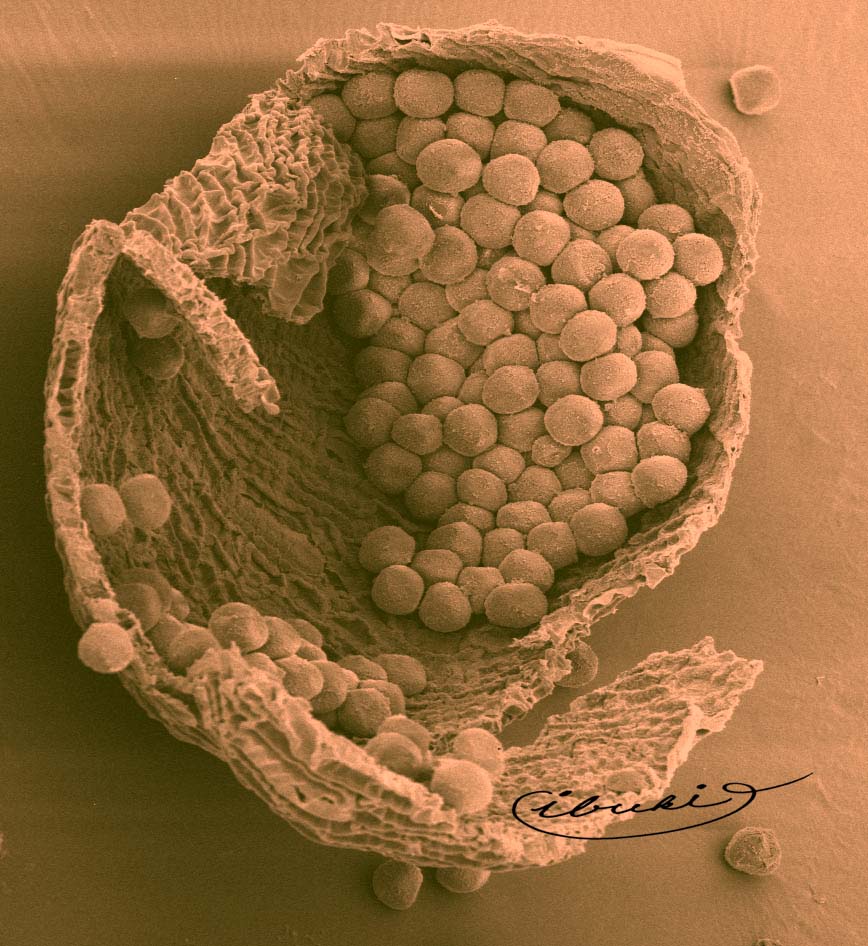 |
| 図2 スギ花粉(着色例1) | 図3 スギ花粉(着色例2) | 図4 スギ花粉(着色例3) |
さて、今回はLUTを使わない別の着色法を紹介します。
LUT法では画像データに応じて特定の色を割り当てますが、ここで紹介する方法は指定の色とSEM画像とをデジタル演算する方法です。SEM画像としては、オリジナルのグレースケール画像でも、LUTで着色した画像でも構いません。この方法は「透明な色フィルタを通してSEM画像を透かせて見る」と表現できると思います。
下記の例(図6)は、図5のグラデーション画像を色フィルターとし、図1のスギ花粉像を重ね合わせたものです。重ね合わせの演算方法には、「リニアライト」を使用しています。
図5の色の塗り方と重ねあわせ演算方法の選択は自由にできます。
 |
 |
| 図5 色フィルター画像 | 図6 スギ花粉(着色例4) |
このように、画面全体の色付け手法だけでも十分に「大人のSEM塗り絵」を楽しめます。
(続く)
その15
波動関数と位相
SEMを作るうえでは電子を粒子とみなしてよい場合が多く、電子の波動関数(特に波面、位相)についてあまり気にしなくてもすみます。
電子レンズの解説書の多くもガラスでできたレンズとの類似性から幾何光学で説明するものが多いです。 ただこの場合、光の屈折率や波面の話をそのまま電子に置き換えて考えることができません。 波面について詳しく知ろうと思うとどうしても量子力学の知識が必要になります。
また薄膜のような位相物体中を通過する電子波動関数の位相変化を知りたくなる場合もあります。
以上から、電子波動関数の位相について私のわかる範囲で概略を説明したいと思います。何らかの参考になればと思います。
シュレーディンガーの波動方程式の解として
ψ(r,t)=a(r) exp[i・ 2π/h・(S(r)-E・t)] ・・・(1)
を考えます。Expの肩のS(r)が空間的な位相を与える部分です。これをシュレーディンガーの波動方程式に代入してある程度の近似を行うと、
{grad S(r)+e A(r)}^2 = g(r)^2 ・・・(2)
注:^は2乗を示す。
が得られます。ここでgrad S(r)というのは、S(r)(すなわち位相)の傾きで、A(r)はベクトルポテンシャルです。
この式は、ベクトルの長さについてだけの式でベクトルの方向は決まりません。それで
grad S(r) - e A(r)= ~g(r) = g(r) ~t(r) ・・・(3)
注:表記~はベクトルを表します。
とおいて~t(r)を求める事を考えます。~t(r)は経路の接線ベクトルです。
ここで下記のpを考えます。
grad S(r)= g(r)~t(r) - e A(r) = p ・・・(3)
pはcanonical momentum、~g(r)はkinetic momentum(mvと表記される場合もあり)と呼ばれます。
ここで最小作用の法則の登場です。作用関数として位相差を使います。すなわち2点間の波動の伝わり方は位相差が最も少なくなるように波動は伝わるという原理です。 2点間(P1からP2)のgrad S(r)の積分が位相差ですから
∫grad S(r)・dr = ∫p・dr = ∫[g(r)~t(r) - e A(r)]・dr
(積分区間はP1からP2まで) (4)
の値が最小になるように~t(r) を求めれば伝搬の仕方がわかります。一般的にはこの計算はとても大変な事と思います。
ここでgは電位ポテンシャルに、e Aはベクトルポテンシャルに依存しますから結局位相差は電界や磁場で変化することを示しています。
以上が、感覚的に位相がどう変化するかを考える場合の基礎です。
2点間の位相差が最小になるように波動が進むことや波動の進行方向t(r)と位相の方向(grad S(r)の方向)はA(r)の存在のために同じ方向ではないところが面白いと感じます。 位相差が最小値(停留値)になるという事は、その近傍で位相があまり変化しない事を意味し、多波合成した場合干渉して消えてしまわないことを意味しているように思います。 またAB効果と呼ばれる不思議な現象も以上から理解できます。
これ以上の説明は今の私の手に負えません。しかしこれだけの理解だけでも考えるヒントになると思います。
詳しくは参考文献をご覧ください。
参考文献:
P.W.Hawkes、E.Kasper :Principles of Electron Optics Vol Ⅲ、ACADEMIC PRESS(1996)
外村彰:電子線ホログラフィー、新オーム文庫、オーム社 (1985)
その16
元祖・電子顕微鏡の作り方(アルデンネ超電子顕微鏡)

本サイトで観察レポートを書いてくださる文ちゃん所有の書籍でしたが、傷みがひどく特別に頼んで再製本していただいた物です。
ドイツ語の訳本で文部省昭和17年2月発行(定価金五円)とあり、まさに戦時下に発刊された本です。
 |
翻訳者のリストには錚々たる日本学術振興会第37電子顕微鏡小委員会の先生諸氏のお名前が並んでいます。透過型、走査型(内容的にはSTEM)のほぼすべての要素に付いて具体的に解説されています。
電子顕微鏡の構造図が実に詳細に書かれていて実物の写真も多く掲載されています。当時、電子顕微鏡を手掛けた人たちはこの本をお手本にして装置を作ったのではないでしょうか。
一例として、対物レンズ周りの構造図を示します。
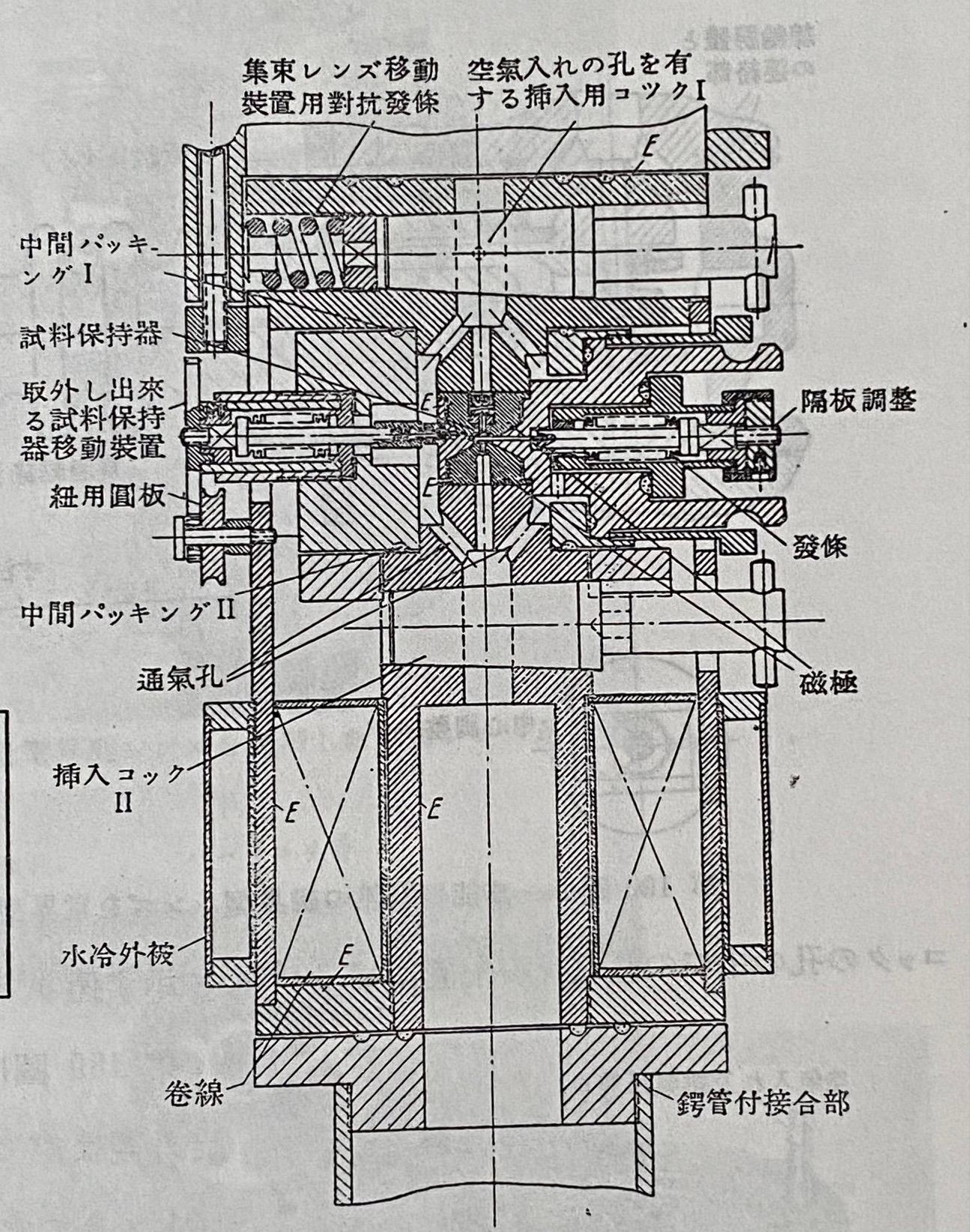 |
「紐用円板」なる用語も見え、ピンと張った紐でプーリーを回し微動機構を動かしている事がわかります。
他の例として、試料交換装置の図を示します。
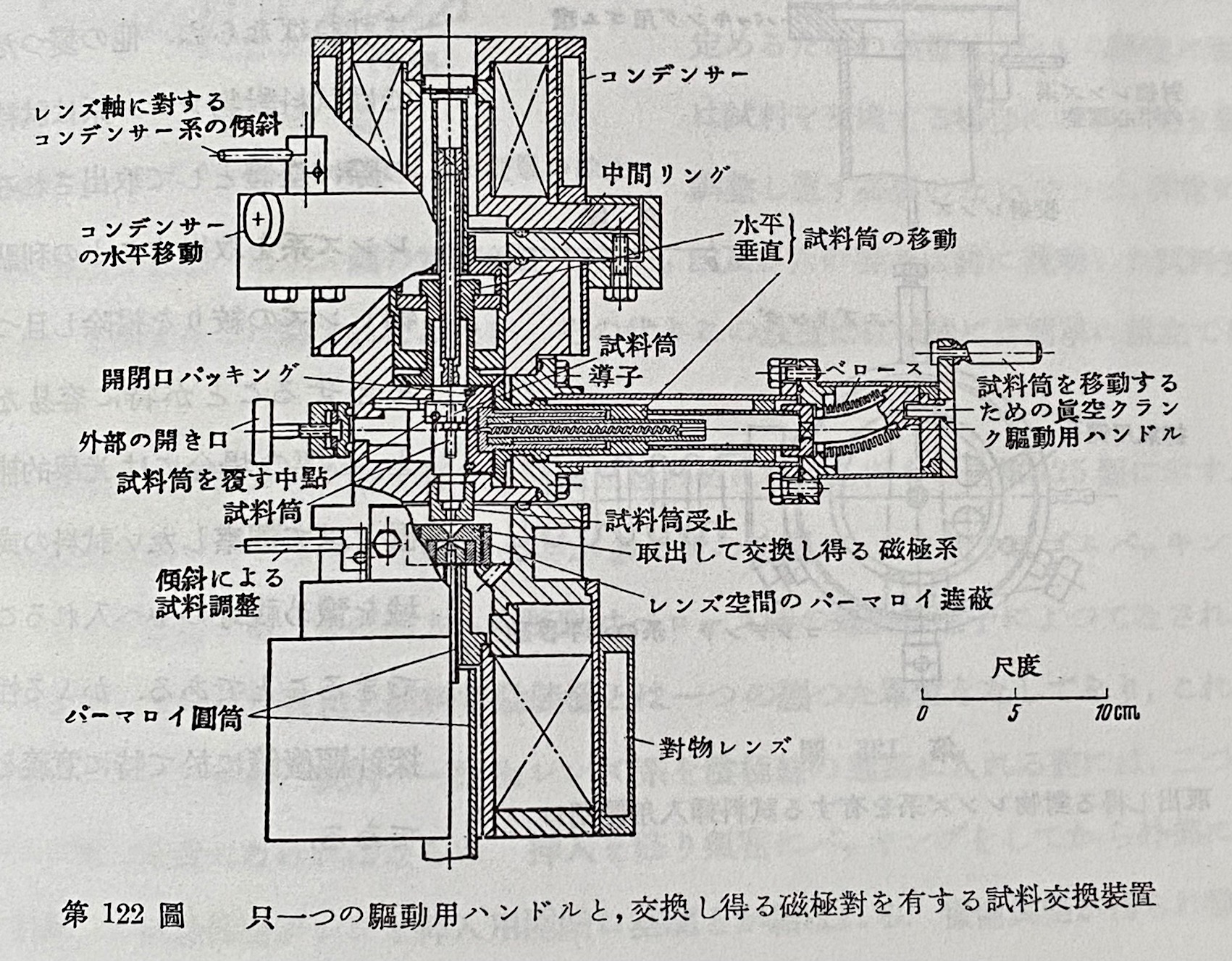 |
図の右方向にあるハンドルを回すだけで、左側から入れられた試料筒は自動的に90度転回し、その後上方から降りてきた中空円筒に押されて所定の位置に収まります。
逆に回すと、全く逆の動きで試料交換室まで試料筒が戻ります。
現代の機構設計用語で、「ヒールスプリングフォロー」と呼ばれる構造ですがとても巧妙な仕掛けです。
電子顕微鏡では精密メカ設計の要素が多く、進歩の激しい電気設計と違い古い文献でもとても参考になります。
話が少しそれますが、精密メカ設計の教科書として私が先輩から譲り受けた同じくドイツ語の本で、BAUELEMENTE DER PHYSIKALISCHEN TECHNIK(物理技術のコンポーネント)という本があります。

これも参考になる図面が多く載っています。以下の例は調整ネジの図面ですが、単にネジを回すだけでもこれだけの方法があるのだと思い知らされます。
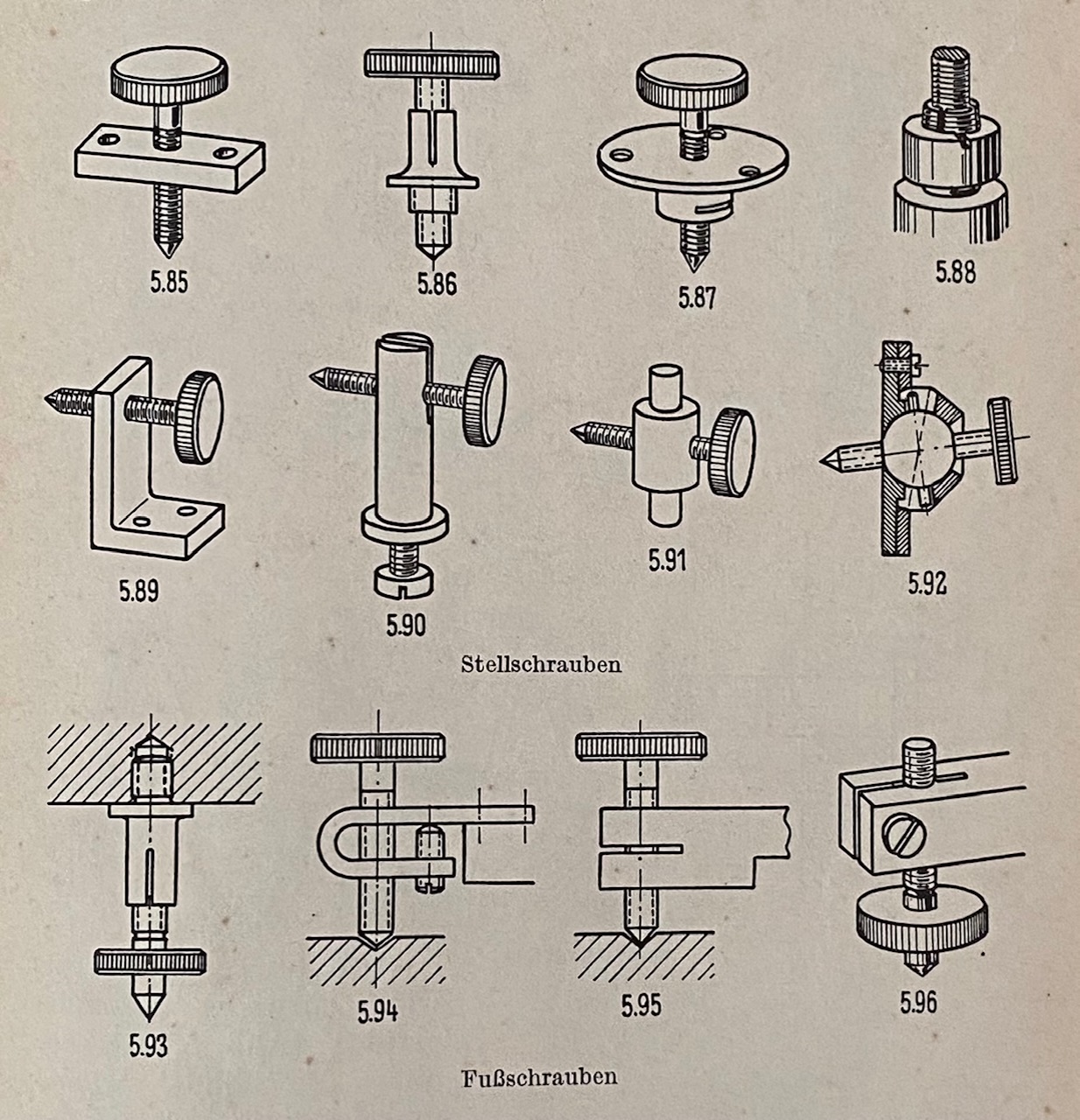 |
ドイツ語が分からなくても図を見るだけでとても勉強になります。
アルデンネの本と並んでドイツの技術力を見せつけられる思いです。
これらの本は図書館で見るしかないと思いますが、もし機会があればご覧になってください。
出典:
(*1)文部省専門学務局訳 : アルデンネ超電子顕微鏡:昭和17年 丸善
(*2)MAX POLEERMANN:BAUELEMENTE DER PHYSIKALISCHEN TECHNIK:
1955, SPRINGER_VERLAG
